And Spirals Everywhere

By Les Tanner

Come on, big guy,” I urged my faithful but laboring vehicle, “you can do it.”

I’m not sure, but I thought I heard a sigh. As much as I liked and trusted my ‘89 SUV, it just didn’t have what it took anymore to go up White Bird grade without a struggle, which was getting to be embarrassing. We were passed as though we were standing still.

Once again I stomped on the gas pedal. Once again came the sigh. As always, though, we finally made it and were able to relax heading downward toward Grangeville.

For those folks who have driven up that grade, you know what I’m talking about. That’s a pretty steep road. Signs warn of stretches of a seven-percent grade. Going up can be hard but so can going down, especially if you’re driving a heavily loaded semi.

I’m sure those drivers are thankful for the emergency pullouts that can slow down and, one hopes, stop runaway vehicles. From what I’ve read, no grades on the U.S. Interstate highway system are steeper than six percent.

Occasionally when I’ve asked folks how steep they think White Bird grade is, the answer has been thirty degrees. Thirty degrees is really steep. More than once my SUV and I, while off-road in 4WD and in very low gear, climbed thirty-degree slopes. But it felt like we were going to fall over backwards.

A seven-percent grade means that the road rises seven feet vertically while traveling one hundred feet horizontally. In ordinary angle measurement that’s four degrees. Just four degrees!  That doesn’t seem like much—unless you’re struggling uphill in a thirty-five-year-old vehicle or racing downhill in a truck whose brakes have failed.

Lima beans in repose. Les Tanner.

Baking flour. Les Tanner.

Granulated sugar. Les Tanner.

Kitty litter. Les Tanner.

Landslide at Jimmy Smith Lake, Custer County. Fredflyfish4, CC-by-3.0

The swirls of an artichoke. Les Tanner.

Dandelion swirls. Les Tanner.

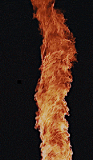
A fire tornado. Manda Lights. CC-by-4.0

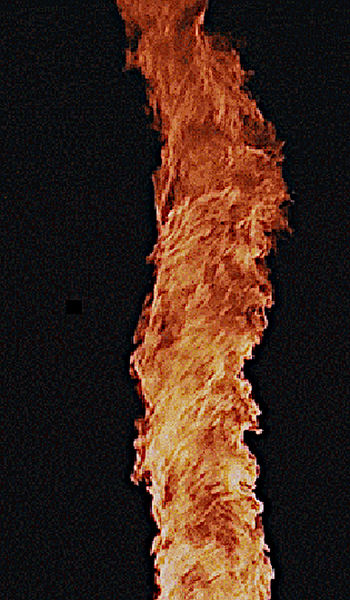
Pine cone swirls. H. Hatch, Pixabay.

A snail shell swirl. Jason Hollinger, CC-by-2.0.

Spider web. Robert Anash, Unsplash.

Spiral galaxies. Pixabay.

Sunflower head. Les Tanner.

Truckload of alfalfa seeds in Parma. Whitney Weber.

Learning about the four-degree angle surprised me, but not in the way I would be if someone were to sneak up behind me and say “Boo!” That’s because as a retired mathematics professor, I’ve long been interested in the math—specifically, the arithmetic and geometry—involved with everyday life.

I’m interested and even fascinated by common shapes and sizes and ages and amounts: The cones of volcanoes, the heights of mountain peaks, the ages of rocks and trees and historic structures, the quantities of deer and squirrels and mosquitoes.

Here are a few number-based Idaho facts I enjoy: The lowest point in the state is 710 feet (the Snake River at Lewiston) and the highest is 12,662 feet (the top of Mount Borah). The state has some 107,651 miles of rivers. The Champion Tree, a giant Western red cedar north of Elk River, is estimated to be more than three thousand years old.

More than two hundred thousand people visit Craters of the Moon every year. As of July 1, 2024, the population of Idaho was 2,001,619. Recent census statistics say the town of Clayton has ten residents.

These days the words million, billion, and trillion are seen or heard everywhere. Everyone says, “I’ve told you a million times” and “thanks a million” but do we know how big a million is?

Actually, I don’t really know, but during a two-week-long winter school break many years ago, I came close. I set my computer to printing out one million dots on regular eight-and-a-half-inch by eleven-inch printer paper. I then glued the resulting pages together to make a chart.

My daughter still has this chart, which is three feet high and forty feet long. I was astounded. I’m glad I didn’t try for a billion dots. The resulting chart would have been forty thousand feet long—that’s more than seven-and-a-half miles. And a chart of a trillion dots?  It would be more than seventy thousand miles long, enough to circumvent the Earth almost three times at the equator.

We’ve all seen piles of sand dumped somewhere. Unless these piles have been disturbed, they’re usually in the shape of inverted cones, the pointy ends up. The sides of the cones slope down from the top at an angle—the famed “angle of repose.” The term refers to the steepest angle at which a pile of material, whether it’s rocks, gravel or sand, can remain stable without the material sliding down.

  An angle of repose exists for anything randomly piled or tumbled. That includes undisturbed piles of snow, talus on a mountain slope, and the rubble that falls from a cliff face or roadside cut. The measure of the angle depends on the material that has fallen or been piled up, and differs from substance to substance. For example, the angle of repose for fallen snow is around thirty-eight degrees.

This means an undisturbed snow slope steeper than thirty-eight degrees is likely to slide down due to gravity. The result is an avalanche. However, snow’s angle of repose varies widely, depending upon its temperature, grain size, moisture content, and the wind conditions. Consequently, folks who monitor avalanche conditions in the Idaho mountains, especially near the state’s many ski slopes, must constantly check those variables.

Seeing helps me believe, so I did some experimentation. I poured four substances—sugar, flour, kitty litter, and lima beans—onto black paper. Indeed, they formed cones, even the lima beans. I took photos, from which I calculated the angles of the cones. I found that flour had the largest angle of repose (thirty-eight degrees) and lima beans the smallest (twenty-two degrees).

A farm near Parma produces alfalfa for the seed. Alfalfa is a plant that has been grown for livestock feed for thousands of years, and fields of the stuff are quite common around Idaho. The seeds are also used to grow alfalfa sprouts which, among other things, are used in salads. In any case, there are markets for the seeds, the largest of which is for planting. The seeds are tiny—a pound of them contains about 240,000 seeds.

A standard truck-load of seeds contains about thirty thousand pounds, which is the output of thirty acres of alfalfa plants. Consequently it takes about an acre of land to produce one thousand pounds of seeds, and since there are about 240,000 seeds in a pound, that means that one acre of plants can produce around 240,000,000 seeds. That’s about one-fourth of a billion seeds.

As a result, it takes four acres to produce a billion seeds–and since a trillion is one thousand times a billion, it takes some four thousand acres to grow a trillion alfalfa seeds—which is about six times the land area of the city of Parma.

I see geometry everywhere in Idaho. Take spirals, for example. Sunflowers. Pine cones. Spider webs. Snail shells. Galaxies. In some cases, as with the spider web and the snail shell, there is a single spiral. In other cases, such as pine cones and sunflowers, there are multiple spirals, some twisting clockwise and some counter-clockwise.

Those spirals have something in common: In each case, the numbers of the spirals coincide with the numbers in the Fibonacci Sequence, named for the Italian who first documented it while studying populations of rabbits. That sequence is 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc. Each number after the first two is the sum of the preceding two: 3=1+2;  5=2+3; 8=3+5, and so on.

 The number of spirals in pine cones and sunflower heads and other similar natural objects will almost universally be one of the Fibonacci numbers. What’s more, when an object has both clockwise and counter-clockwise spirals, such as a pine cone, the total numbers of those opposite spirals are two consecutive Fibonacci numbers.

  When I first learned that, it brought a definite “Wow!” Just as I’d done with the angle of repose stuff, I experimented on my own. Several years ago, I grew a sunflower  whose head was twelve inches in diameter. I counted the spirals in each direction, and marked every fifth spiral. There were fifty-five counter-clockwise spirals and eighty-nine clockwise spirals: both of them Fibonacci numbers.

Many other plants exhibit spirals, including all sorts of flowers, artichokes, pineapples— even the needles on a pine bough are arranged in spirals. As I was writing this story, the news showed that very hot fires like those raging in California could generate tornado-like spirals of burning material that could
spread fires far from the original source.

 I think one reason why such things fascinate me is that numbers and shapes are a large part of what mathematics is about. It’s basically the study of patterns.Such patterns lead to formulas and equations that can be used to predict future events. People regard those formulas and equations as mathematics but the truth is that math is around us every day. All you need to do is look.

That said, I’ve got some cool stuff at my place you won’t see every day. Things like tensegrity structures, and my favorite “wow,” a bit of arithmetic I call “four numbers.” I’m happy to show anyone who will listen. If you come to Caldwell, just look for the guy in the orange hat, no spirals.